杭电acm入门

Tanpinsary2025-01-252025-08-15

第一讲数学基础

before: 多组输入的处理

输入处理

类型一：输入不说明有多少input block，默认以**EOF**为读入结束

例1：A+B Problem

#include <stdio.h>
int main()
{
	int a, b;
	while(scanf("%d %d", &a, &b) != EOF) 
		printf("%d\n", a + b);
	return 0;
}

scanf函数的返回值为成功输入的变量个数，无读入返回**EOF（为-1**，而非0），因而我们还可以这样：

#include <stdio.h>
int main()
{
	int a, b;
	while(scanf("%d %d", &a, &b) == 2) 
		printf("%d\n", a + b);
	return 0;
}

若使用cpp，更加方便

1
2
3

while(cin >> a >> b) {
	...
}

类型二：输入开始告知有N个Input Block

先读入N，在借助while或者for循环实现

类型三：不说明有多少Input Block，但是以特殊输入为结束标志

处理方式类似类型一——先读

仍然以A+B Problem为例，当a与b均不为0时结束

#include <stdio.h>
int main()
{
	int a, b;
	while(scanf("%d %d", &a, &b) != EOF && (a != 0 || b != 0)) 
		printf("%d\n", a + b);
	return 0;
}

更好地：（可读性更好）

while(scanf("%d %d", &a, &b)) {
	if(a == 0 && b == 0)	break;
    printf("%d\n", a + b);
}

类型四：前三种的组合问题
类型五：字符串的输入问题

例：HDOJ_1048

若c：

1
2
3

char buf[20];
gets(buf);
// 不安全的读入，不推荐！

若cpp：

//如果用 string buf; 来储存
getline(cin, buf);
//如果用 char buf[255]; 来保存
cin.getline(buf, 255); //cin的成员函数

输出处理

类型一：每个Input Block对应一个Output Block，Output Block之间没有空行
类型二：每个Input Block对应一个Output Block，Output Block之后有一个空行
类型三：每个Input Block对应一个Output Block，Output Block之间有一个空行

小差别注意即可

注意：

多组数据，是否需要一次性全部读取，再一组一组处理？

不需要

提交到OJ的程序从文件中读取，然后生成临时文件存储输出，与标准Output进行逐字符对比处理

导引：整数求和( $N \leq 500000$ )

等差数列的公式求和的风险？
$sum(n) = n \times (n - 1) / 2$ $s u m (n) = n \times (n - 1) /2$ ，N过大时， $n \times (n-1)$ $n \times (n - 1)$ 会爆`int`(32位)
解决方案：
- 64位整数(long long, %lld)

例一：求最小公倍数

暴力枚举？TLE
数学方法： $LCM(A,B)=A \times B/GCD(A,B)$

注意点同导引，如何防止过程中爆int？先÷后x
$LCM(A,B)=A/GCD(A,B) \times B$

求GCD？辗转相除法（欧几里得算法）

$O(\log n)$ 级的算法
原理
终止条件：有一方为0，另一方为gcd

int gcd(int a, int b) {
    int temp;
    while(b != 0) {
        temp = a % b;
        a = b;
        b = temp;
    }
    return a;
}

为什么不需要在意大小？第一轮处理会交换

1
2
3

//递归写法
int gcd(int a, int b)
    return (b != 0) ? gcd(b, a % b) : a;

例二：计算N个N相乘的个位数——规律

（ $1 \leq N \leq 1,000,000,000$ )
暴力（TLE）
每次处理后模10？——解决了数据溢出，但是循环次数仍然太多
找到规律循环节，后打表

为什么去找规律？

数据规模太大
暴力计算不可行

例三：特别的fibonacci数列——规律与循环节

F(0) = 7

F(1) = 11

F(n) = F(n-1)+F(n-2)\quad(n > 3)

给定一个n(n<1000000)，请判断F(n)能否被3整除，分别输出yes和no

递归计算每一项，模3 数据规模太大
同余定理： $F(n)\%3=F(n-1)\%3+F(n-2)\%3$
规律：发现循环节

G(1) G(2) G(3) G(4) G(5) G(6) G(7) G(8) G(9) G(10) G(11)

1 2 0 2 2 1 0 1 1 2 0

循环节为8
为什么一定会有循环节？

——抽屉原理

由于%3结果一定是0 1 2，且前两项导出后一项，考虑所有相邻两项的组合，共有9种组合，且0 0情况可排除，即8种，则根据抽屉原理（容斥原理），则循环节在大致9位内会出现，一旦出现了重复的相邻两项，则一定出现了循环节

G(1)	G(2)	G(3)	G(4)	G(5)	G(6)	G(7)	G(8)	G(9)	G(10)	G(11)
1	2	0	2	2	1	0	1	1	2	0

例四：求A^B最后三位数表示的整——快速幂

找规律不可行样本太大了

快速幂（二分加速）

递归实现

int power(int a, int n) {
      int ans;
      if(n == 0)
          ans = 1;
      else {
          ans = power(a * a, n / 2);
          if(n % 2 == 1)
              ans *= a;
      }
      return ans;
  }

非递归实现

int power(int a, int n) {
    int ans = 1;
    while(n) {
        if(n % 2)
            ans *= a;
        a = a * a;
        n /= 2;
    }
    return ans;
}

特别注意：小心爆**int**!!
快速幂基本都伴随着取模运算

第二讲贪心算法

总是做出当前来看的最优解
分解子问题，对子问题按照同样的策略进行操作

例一：田忌赛马

已知田忌与国王所有马的能力值，赢的人获得200元，如何找到最优解？

贪心策略

用自己的马挑战对方比自己弱的最小的马
确定思路
- 排序
- 比较未标记的最好的马，自己的能超过对方的马吗
  - 如果可以，则赛马
  - 如果不可以，则用自己最差的马和对方最好的马赛马
  - 赛马做标记
- 重复策略直至所有的马比完

例二：事件序列问题

贪心策略

拿结束时间排序，尽量留出更多的时间
确定思路
- 提出命题：至少存在一个最长的事件序列，包含最早结束的事件
  - 证明：反证法
    
    逆命题：所有的最长事件序列都不包含最早结束的事件
    
    在该假设下任取一个最长的事件序列，将第一个事件与最早结束的事件替换，则构造了一个相同长度的最长的时间序列且含有最早结束的事件，逆命题不成立，原命题得证
- 按照结束时间排序
- 找到最早结束事件作为第一个事件
  
  此时问题分解为n-1阶的子问题，注意额外分析是否会冲突
- **注意！！**选出的结果方案不唯一，而方案的序列长度一定唯一

例三：搬桌子

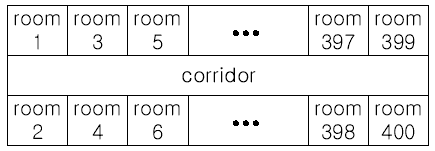
丁爸信奥培训中心最近在富丽科技大厦租了一层楼，这层楼的形状如下：

由图可见，这层楼中间是走廊，两侧各有200个房间，编号如上图。

最近，丁爸信奥培训中心做了内部机构的调整，需要把一些桌子从一个房间搬到另外的房间。因为走廊很窄，但是桌子很大，所以同一段走廊每次只能通过一个桌子。假设不论远近，每趟搬桌子都需要10分钟。同时，当你从房间i搬桌子到房间j的过程中，房间i到房间j之间的走廊都被占用，也就是说，在每个10分钟内，不能有多个任务共享同一段走廊。

现在，丁爸想知道：要完成所有的搬运任务，最少需要多少时间？

问题分析：
- 为什么不能找多次最长事件序列？
  
  最长事件序列只能保证单一最优解，全局并非最优解

贪心策略

最优策略：记录路径，找到重叠最多地方的重叠次数，即为所需最多的次数

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
int p[201];
int main() {
    int T, ans;
    cin >> T;
    while(T --) {
        int n;
        cin >> n;
        int s,t;
        memset(p, 0, sizeof(p));
        ans = 0;
        for(int i = 0; i < n; i ++) {
            cin >> s >> t;
            s = (s + 1) / 2;
            t = (t + 1) / 2;
            if(s > t)
                swap(s, t);
            for(int j = s; j <= t; j++)
                p[j]++;
        }
        for(int i = 1; i <= 200; i ++)
            if(p[i] > ans)
                ans = p[i];
        cout << ans * 10 << endl;
    }
    return 0;
}

较差策略：按照开始位置排序，从第一个需要搬的桌子开始i，一次性找到所有线路不冲突的桌子，不断分解子问题

#include<stdio.h>
#include<vector>
#include<iterator>
#include<algorithm>
using namespace std;
struct M{
	int s;
	int t;
};

bool comp(const M &m1, const M &m2){
	return m1.s < m2.s;	//按照开始的房间号排序
}

int main(){
	int T, s, t;
	scanf("%d", &T);
	while(T--) {
		int n;
		vector<M> v;
		scanf("%d", &n);
		for(int i = 0; i < n; ++i) {
			M m;
			scanf("%d%d", &s, &t);
			if(s > t)//有可能从号码大的房间往回搬，若是，则交换s与t
				swap(s, t);
			m.s = s;
			m.t = t;
			v.push_back(m);
		}
		sort(v.begin(), v.end(), comp);
		int ans = 0;
		for(vector<M>::iterator it = v.begin(); it != v.end();){	//从房间号最小的开始查找
			++ans;
			int t = (*it).t;
			for(vector<M>::iterator subit = it; subit != v.end();) {	//找到与要搬的线路不冲突的桌子
				if((*subit).s > t && !((*subit).s - t == 1 && (*subit).s % 2 == 0)) {	//注意对面房间的线路也是冲突的，比如5与6
					t = (*subit).t;
					subit = v.erase(subit);	//该桌子已搬完，删除
				} else
					 ++subit;	//否则继续查找下一张桌子
			}
			it = v.erase(it);	//删除
		}
		printf("%d\n", ans * 10);
	}
	return 0;
}

例四：删数问题

有一个长度为n（n <= 240）的正整数，从中取出k（k < n）个数，使剩余的数保持原来的次序不变，求这个正整数经过删数之后最小是多少。

子问题分解：每一次删除数字都使得剩下的正整数保持最小
贪心策略：

删除从左向右第一个逆序列的第一个数字

或删除从左到右递增序列结束处的数字

#include<bits/stdc++.h>
using namespace std;

int main() {
	string str;
	int k, flag = 0;
	vector<char> v;
	
	cin >> str >> k;
	
	for(int i = 0;  i < str.size(); i++){
		v.push_back(str[i]);
	} 
	
	while(k--){
        int i = 0;
        flag = 0;
        vector<char>:: iterator t = v.begin();  //这里主要是为了调用  v.erase()的库函数删除元素
        while(i != v.size() - 1) {  //注意这里的减一 因为下方的v[i+1] 否则会出现段错误
            if(v[i] > v[i + 1]) {  //如果出现后一个数小于前一个数那么这就是这一趟的递增的终点 
                v.erase(t);
                flag = 1;
                break;
            }
            i++;
            t++;
		}
		
		if(flag == 0) {//如果是一个递增序列那么的话就要删除最后一个数 
			v.erase(t);
		}		 
	} 
	int i = 0;
    //这么输出是为了防止前置'0'的输出
	for(int i = 0; i < v.size(); i++)  {
		if(v[i] != '0')
			break; 
	}	
	for(int j = i; j < v.size(); j++){
		cout << v[j];
	} 	
}

例五：青蛙的邻居

未名湖附近共有N个大小湖泊L1, L2, …, Ln(其中包括未名湖)，每个湖泊Li里住着一只青蛙Fi(1 ≤ i ≤ N)。如果湖泊Li和Lj之间有水路相连，则青蛙Fi和Fj互称为邻居。现在已知每只青蛙的邻居数目x1, x2, …, xn，请你给出每两个湖泊之间的相连关系。

Input

第一行是测试数据的组数T(0 ≤ T ≤ 20)。每组数据包括两行，第一行是整数N(2 < N < 10)，第二行是N个整数，x1, x2,…, xn(0 ≤ xi ≤ N)。

Output

对输入的每组测试数据，如果不存在可能的相连关系，输出"NO"。否则输出"YES"

离散数学：可图形判定
- 度序列
  
  若把一个图G所有顶点的度数台城一个序列S，则称S为图G的度序列
- 度序列是可图的
  
  一个非负整数组成的有限序列如果是某个无向图的度序列，则称该序列是可图的
- Havel-Hakimi定理
  
  由非负整数组成的有限非递增序列， $S=\{d1,d2,d3...dn\}$ ，当且仅当 $S1=\{d2-1,d3-1...d(d1+1),d(d1+2)......dn\}$ 也是可图的
贪心策略：

通过havel-hakimi定理，对序列由大到小排序，然后对 $S_1$ 操作，排序，对 $S_2$ 操作，排序……直到序列全部变成0。如果出现负数，则该度序列是不可图的

第三讲并查集

导引问题

在某个城市里住着n个人，现在存在关于n个人的m条信息，假设所有认识的人为一个单位，最多有多少个单位

什么是并查集

Disjoint Set，即“不相交的集合”

N个元素的N个对象划分为不相交集合，每个集合中选定某个元素代表所在集合
常见两种操作
- 合并两个集合
- 查找某个元素属于哪个集合

实现方法一

用编号最小的元素标记所在集合
定义一个数组 $Set[1..n]$ ，其中 $Set[i]$ 表示元素 $i$ 所在集合

Set(i) 1 2 1 4 2 6 1 6 2 2

i 1 2 3 4 5 6 7 8 9 10

不相交集合：
$\{1, 3, 7\}, \{4\}, \{2, 5, 9, 10\}, \{6, 8\}$

Set(i)	1	2	1	4	2	6	1	6	2	2
i	1	2	3	4	5	6	7	8	9	10

两个功能

查 $O(1)$
1
2
int find(x)
return Set[x];

并 $O(n)$

void Merge(a, b) {
    int i = min(a, b);
    int j = max(a, b);
    for(int k = 1; k <= N; k++) {
        if(Set[k] = j)
            Set[k] = i;
    }
}

实现方法二——树

利用树实现
定义数组 $Set[1..n]$
- 若 $Set[i] = i$ ，说明 $i$ 表示该集合，是该集合的对应树的根
- 若 $Set[i] = j$ ，说明 $j$ 是 $i$ 的父节点
两个功能
- 查最坏 $O(n)$
  1
  2
  3
  4
  5
  6
  int find(x) {
  int r = x;
  while(Set[r] != r)
  r = Set[r];
  return r;
  }
- 并 $O(1)$
  1
  2
  void merge(a, b)
  Set[a] = b;
- 避免出现最坏情况
  - 方法：将深度小的树合并到深度大的树
  - 实现：假设两棵树的深度 $h_1$ , $h_2$ ，则合并后的树的高度为
    $h = \begin{cases} \max(h_1, h_2) & \text{if } h_1 \neq h_2 \\ h_1+1 & \text{if } h_1=h_2 \end{cases}$
  - 效果：任何顺序的合并操作后，包含k个节点的树的最大高度不超过 $\log k$
- 优化后
  1
  2
  3
  4
  5
  6
  7
  8
  9
  void merge(a, b) {
  if(height[a] = height[b]) {
  height[a]++;
  Set[b] = a;
  } else if(height(a) < height(b))
  Set[a] = b;
  else
  Set[b] = a;
  }
  此时，查的效率已经变为最坏 $O(\log n)$

实现方法三——带路径压缩的查找操作

int find(x) {
    if(Set[x] != x)
        Set[x] = find(Set[x]);
    return Set[x];
}

例一

经典案例：最小生成树

Prim算法
Kruskal算法
- 理论基础——MST性质
  
  命题：至少存在一颗最小生成树含有权值最小的边
证明：类似第二讲例二的证明
- 算法步骤：（贪心算法）
  - 选中最小的边
  - 找到下一个最小的边，若两个顶点不连通，则选中，重复
  - 直到选中 $n-1$ 条边

例二

第四讲递推求解

递推关系式（状态转移方程）

将 $F(n)$ 用 $F(n-1)$ 与增减量表示可能与前面的多项有关系

例一——状态产生分析

一个平面上有 $n$ 条直线，这些直线中每一条在圆内同其他直线相交，假设没有三条直线相交，试问能分成多少区域

分析：假设此时有n-1条直线分割圆，令第n条直线把上述n-1条直线分割产生n-1个端点，n条线段，即可分割产生n个新区域

初始状态： $F(1)=2$

状态转移方程： $F(n)=F(n-1)+n$

例二

平面上有 $n$ 条折线，这些折线最多能将平面分割为多少块？

分析：假设此时有n-1条直线分割平面，第n条折线可以做到与前n-1条折线都产生四个交点

状态转移方程： $F(n)=F(n-1)+4(n-1)+1$

例三——状态向前分析

在 $2\times n$ 的长方形方格中，用n个 $1\times 2$ 的骨牌铺满方格，有多少种铺设的方案

例一与例二都是从状态产生的角度去思考状态转移方程
然而例三给出了另一种思考方式

从第 $n$ 个状态向前分析成因

第n列格子分为横竖两种状态

若为竖，则前有F(n-1)种状态

若为横，则n列和n-1列为双横，前有F(n-2)种状态，故：

状态转移方程： $F(n)=F(n-1)+F(n-2)$
核心：大问题分类讨论分别解决

例四

有 $1 \times n$ 的长方形，用 $1\times 1$ ， $1\times 2$ ， $1\times 3$ 的骨牌铺满方格，求第n个多少种铺法

分析同例三

状态转移方程： $F(n)=F(n-1)+F(n-2)+F(n-3)$

总结

首先：确认能否容易得到初始状态的解
假设：规模不大于 $N-1$ 的状态已经得到了解决
最后：重点分析当规模扩大到 $N$ 时，如何枚举当前的情况，然后用子问题生成

例五——合法性角度分类

所有学生站成一排，规定女孩不能单独站，即要么队列中没有女生，要么不止一个女生并排站

比如， $n=4$ 时，有下面合法队列：

FFFF、FFFM、MFFF、FFMM、MFFM、MMFF、MMMM

给定人数 $n$ 求可能的合法队列数

两种做法，一种分男女考虑合法与非法状况
另一种设计子函数分别表示男女来生成

\text{状态转移方程}\qquad F(n)=F(n-1)+F(n-2)+F(n-4)

例六

有排成一行的 $n$ 个方格，用R，P，G三色进行涂色，每格涂一种颜色，要求航信放个不能同色，首位两格也不能同色

依旧是合法性分类

状态转移分析：

前n-1格子序列合法的情况： $F(n-1)$ 此时第n个格子不能与合法的第一个和第n-1个颜色相同，只能有一种选择
前n-1格子序列非法的情况： $2F(n-2)$ 若想在第n个格子添加后生成合法的格子序列，该非法类型只能是第一个格子与第n-1个格子同色这一部分的非法序列来源于合法的n-2序列添加一个首色格子，为 $F(n-2)$ 此时的最后一个格子有两种颜色可以选择

故： $F(n)=F(n-1)+2F(n-2)$

例七

$2\times n$ 个数字按照顺时针方向围成一个圆， $n$ 条线段把所有数字两两相连，要求不能有交叉
求：有多少合法的连线方案

卡特兰数列(Catalan)

1、2、5、14、642、132，……
$c[0]=1$ $c[n]=\sum_{i=0}^{n-1}c[i]c[n-1-i]$ $\Rightarrow c[n]=\frac{C_{2n}^{n}}{n+1}$
高精度组合问题

第五讲动态规划

典例1

![[Pasted image 20250225215005.png]] 有如上数塔，从顶部出发，在每一个节点都可以选择向左走或者向右走，一直走到底层，要求找到一条路径善意的路径上数值和最大

首先考虑暴力求解，如何遍历所有路径，显然有 $2^{n-1}$ 条路径，不予考虑
分解子问题：从顶点开始考虑左右两侧的最优解（类似二叉树考虑左右子树的最好情况）时间复杂度： $O(n^2)$
结论：自顶向下的分析，自底向上的计算

例一：免费馅饼

数轴上可能在某一时刻在某一位置掉落免费馅饼，0秒时人在5m处，每秒钟人只能移动一米，给出馅饼掉落的位置与时刻，给出获得馅饼最多的最优解

显然问题仍然在于分解时间寻找最优解，问题是如何分解？
注意到人的操作只有向左或向右或停止不动，那么将一维的数轴按照时间作为第二个轴进行绘图，发现其实就是数塔问题

典例二：最长有序子序列

I	0	1	2	3	4	5	6	7	8
Num[I]	1	4	7	2	5	8	3	6	9

如何分解子问题？
考虑到序列的寻找是从无至有的，也就是可以将问题规模从小到大考虑

I	0	1	2	3	4	5	6	7	8
Num[I]	1	4	7	2	5	8	3	6	9
F[I]	1	2	3	2	3	4	3	4	5

F[I]

为以

Num[I]

为序列结束数字的最大长度，也就是将规模为n的问题分解为n个子问题分别计算，再进行比较即可

核心思想：利用已经解决的子问题作为已知条件进行演算后续问题（即：站在巨人的肩膀上看问题）

例二：胖老鼠问题

给出若干个老鼠的体重和速度，找到一个最长的序列，使得体重越来越大，速度越来越低

按照体重递增排序，然后按照速度降序的原则寻找最长递减有序子序列

例三：最少拦截系统

给出n个飞弹，并且给出这n个飞弹的高度，有拦截系统进行拦截，且拦截系统拦截的多个导弹的高度只能递减

1：一套拦截系统最多可以拦截几个导弹？仍然是最长不递增有序子序列问题 2：最少需要几套拦截系统才能拦截所有导弹？

尝试模拟？单次都做到拦截最多——贪心算法
问题的本质：最少分成几个”最长不递增有序子序列问题“
- Dilworth定理：对于一个偏序集，最少链划分数等于最长反链长度
- 结论：本体的本质为求最长上升子序列的长度

例四：搬宿舍

搬宿舍，只能左手一个右手一个，搬东西消耗的能量为两者质量差的平方成正比。已知有n个物品，需要搬k次，分别给出所有的物品重量，求消耗的最少能量

第一感觉：两手的东西质量尽可能接近
粗略思考验证：搬运一次必须要搬运质量相邻的两者
预处理：排序
问题的分解：搬运k次的最优解建立前k-1次的最优解情况，考虑递推，考虑dp
设 $F(n.k)$ 为在前n个物品中搬运k次，则可以分解问题

F(n,1)=\min \begin{cases} (x_n-x_{n-1})^2\\ F(n-1,1) \end{cases}

如果拓展到 $F(n,k)$ 呢？其实还是在分解问题，搬运第k次有两种，一种是这k次搬走了第n个物品，一种是没有，那么状态转移方程按照上述的思路即可解决：

F(n,k)=\begin{cases} (x_n-x_{n-1})^2+F(n-2,k-1)\\ F(n-1,k) \end{cases}

注意问题的初始状态：问题规模在 $F(4,2)$ 以下的都可以作为初始状态， $F(4,2)$ 的解显然为 $(x_1-x_2)^2+(x_3-x_4)^2$

小结：

基本思想：如果各个子问题不是独立的（即：重复的），不同的子问题的个数只是 多项式量级 （即：有限的），如果我们能用数组来保存已解决的子问题的答案，在需要时直接获取已求得的答案，这样就可以避免大量的重复计算
特点：
- 最优子结构 大问题的最优解一定包含子问题的最优解
- 重叠子问题 子问题是重叠的，即大规模问题的解决牵扯到小规模问题
- 无后效性 完成小规模问题后再完成大规模问题的时候，大规模问题的解决不会影响小规模的问题

第六讲背包问题

导引问题

现有一张餐券面值10元，有菜肴N种，餐券一次性使用不可找零，问如何选择菜肴使得餐券使用最不浪费

什么是背包问题

给定容量为 $V$ 的背包和若干物品，在一定的限制条件下问最多能放进多少价值的物品
最经典的DP问题
背包问题中状态的理解（状态与状态转移）

背包问题分类

01背包（非常重要！！！）
完全背包
多重背包
二维费用背包
混合三种背包
分组背包
有依赖的背包

01背包

特点：每种物品仅有一个
有 $N$ 个物品和一个容量为 $V$ 的背包，第 $i$ 件物品的费用是 $c[i]$ ，价值是 $w[i]$ ，求解放入哪些物品使得价值总和最大
问题特点：每种物品仅有一件，仅能选择放or不放
子问题分解？ —— 基于状态
无须→有序？从 $1$ 到 $i$ 依次考虑各个物品
状态定义： $f[i][v]$ 表示考虑前 $i$ 件物品后放入一个容量为 $v$ 的背包可以获得的最大价值

例一

张三喜欢收集骨头，每个骨头有自己的价值和体积，求问背包可以装下最多价值的物品例如：体积为10，有5块骨头，价值分别为1，2，3，4，5，体积分别为5，4，3，2，1

仍然采取第五讲例四的思路
从前0个物品依次考虑前 $i$ $i$ 个物品，按照这个顺序从背包体积为0到10依次进行分析
1. 没装第 $i$ 个物品——价值为 $d[i-1][v]$ （继承上一行的价值）
2. 装第 $n$ 个物品——此时的背包容量相比上一行能否放得下？如果放得下，放入并计算价值
以上两个情况取 max 记录这个格子内
得到了下面的表格（程序的执行过程即为从第一行到最后一行一次从左向右遍历

$(Y,C)$	1	2	3	4	5	6	7	8	9	10
0	0	0	0	0	0	0	0	0	0	0
$(1,5)$	0	0	0	0	1	1	1	1	1	1
$(2,4)$	0	0	0	2	2	2	2	2	3	3
$(3,3)$	0	0	3	3	3	3	5	5	5	5
$(4,2)$	0	4	4	4	7	7	7	7	9	9
$(5,1)$	5	5	9	9	9	12	12	12	12	14

二维背包最能反映01背包的本质——考虑前1个，前2个，前3个……前i个，当背包体积最大时，得到的结果就是最优解
状态转移方程：

DP[i][j]=\max(DP[i-1][j],DP[i-1][j-v[i]]+w[i])

时间复杂度与空间复杂度都为 $N \times V$

空间复杂度的优化：使用一维数组DP[j]，从后向前遍历

1
2
3

for i = 1 to n
    for j = V to v[i]
        dp[j] = max(dp[j], dp[j-v[i]] + w[i])

完全背包

特点：一种物品可以取无数个
可否转化为01背包？

多重背包

二进制优化

//预处理
int t = 1;
while(x >= t) {
	v[cnt] = a * t;
	c[cnt++] = b * t;
	x -= t;
	t <<= 1; //按照2^k打包
}
if(x) {   //剩余打包
	v[cnt] = a * x;
	c[cnt++] = b * x;
}

二维费用背包

第七讲 BFS入门

预备知识队列 stl queue

层次遍历

二叉树
图

例

BFS标准套路

第八讲 DFS入门

导引递归

特征：
- 先写出口（不需递归的特殊情况）
- 再写普遍情况（递归解决）

例一全排列

递归特征：
- 如果第一个数确定，则剩余问题就是其余 $n-1$ 个数字的全排列
- 如果前 $k$ 个数确定，则剩余问题就是其余 $n-k$ 个数字的全排列
- 枚举当前的每一种情况
  - 在每一种可能中，递归调用dfs(step + 1)

#include<bits/stdc++.h>
using namespace std;
int vis[10], num[10];
int n;

void dfs(int step) {
	if(step == n + 1) {
		for(int i = 1; i <= n; i++)
			cout << a[i] << " ";
		cout << endl;
	}
	for(int i = 1; i <= n; i++) {
		if(vis[i] == 0) {
			num[step] = i;
			vis[i] = 1;
			dfs(step + 1);
			vis[i] = 0;  //回溯 
		}
	}
} 

int main() {
	while(cin >> n)	{
		memset(vis, 0, sizeof(vis));
		dfs(1);
	}
	return 0;
}

图解（图源自dfs深度搜索全排列图解详细步骤（图解版） - 白色飞碟 - 博客园大佬太牛了）

第一讲 数学基础

before: 多组输入的处理

输入处理

类型一：输入不说明有多少input block，默认以**EOF**为读入结束

类型二：输入开始告知有N个Input Block

类型三：不说明有多少Input Block，但是以特殊输入为结束标志

类型四：前三种的组合问题

类型五：字符串的输入问题

输出处理

类型一：每个Input Block对应一个Output Block，Output Block之间没有空行

类型二：每个Input Block对应一个Output Block，Output Block之后有一个空行

类型三：每个Input Block对应一个Output Block，Output Block之间有一个空行

导引：整数求和(N≤500000N \leq 500000N≤500000)

例一：求最小公倍数

例二：计算N个N相乘的个位数——规律

例三：特别的fibonacci数列——规律与循环节

例四：求A^B最后三位数表示的整——快速幂

第二讲 贪心算法

例一：田忌赛马

例二：事件序列问题

例三：搬桌子

例四：删数问题

例五：青蛙的邻居

第三讲 并查集

导引问题

什么是并查集

实现方法一

实现方法二——树

实现方法三——带路径压缩的查找操作

例一

经典案例：最小生成树

例二

第四讲 递推求解

例一——状态产生分析

例二

例三——状态向前分析

例四

总结

例五——合法性角度分类

例六

例七

第五讲 动态规划

典例1

例一：免费馅饼

典例二：最长有序子序列

例二：胖老鼠问题

例三：最少拦截系统

例四：搬宿舍

小结：

第六讲 背包问题

导引问题

什么是背包问题

背包问题分类

01背包

例一

完全背包

多重背包

二维费用背包

第七讲 BFS入门

层次遍历

例

第八讲 DFS入门

导引 递归

例一 全排列

例二 迷宫搜索

第八讲 二分匹配

经典算法：匈牙利算法

变式一：最小定点覆盖

Tanpinsary

第一讲数学基础

类型一：输入不说明有多少input block，默认以`EOF`为读入结束

导引：整数求和( $N \leq 500000$ )

第二讲贪心算法

第三讲并查集

第四讲递推求解

第五讲动态规划

第六讲背包问题

导引递归

例一全排列

例二迷宫搜索

第八讲二分匹配